2021년04월17일 18번
[과목 구분 없음] 그림과 같은 직사각형 균질단면에서 x축에 대한 회전반경(rx), 탄성단면계수(Sx), 소성단면계수(Zx), 형상계수(f)를 각각 계산한 결과로 옳은 것은?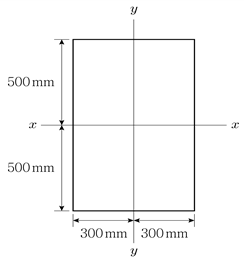

- ① 회전반경(rx)=500√3 mm
- ② 탄성단면계수(Sx)=109mm3
- ③ 소성단면계수(Zx)=1.5×108mm3
- ④ 형상계수(f)=0.85
(정답률: 41%)
문제 해설
회전반경(rx)은 직사각형 균질단면에서 x축에 대한 중심선과 단면의 최대거리를 의미합니다. 이 경우, x축에 대한 중심선과 단면의 최대거리는 500mm이므로, 회전반경(rx)=500√3 mm입니다.
탄성단면계수(Sx)는 단면이 얼마나 강하게 변형에 저항하는지를 나타내는 값으로, 단면의 넓이와 회전반경의 제곱을 나눈 값입니다. 이 경우, 단면의 넓이는 1000mm × 500mm = 500000mm2이므로, 탄성단면계수(Sx)=109mm3입니다.
형상계수(f)는 단면의 형상이 원형에 가까울수록 1에 가까워지는 값으로, 이 경우에는 0.85로 주어졌습니다.
소성단면계수(Zx)는 단면이 얼마나 강하게 파괴에 저항하는지를 나타내는 값으로, 단면의 넓이와 회전반경의 제곱을 나눈 값에 형상계수를 곱한 값입니다. 이 경우, 단면의 넓이는 1000mm × 500mm = 500000mm2이고, 회전반경(rx)=500√3 mm, 형상계수(f)=0.85이므로, 소성단면계수(Zx)=(500000mm2 / (500√3 mm)2) × 0.85 = 1.5×108mm3입니다.
탄성단면계수(Sx)는 단면이 얼마나 강하게 변형에 저항하는지를 나타내는 값으로, 단면의 넓이와 회전반경의 제곱을 나눈 값입니다. 이 경우, 단면의 넓이는 1000mm × 500mm = 500000mm2이므로, 탄성단면계수(Sx)=109mm3입니다.
형상계수(f)는 단면의 형상이 원형에 가까울수록 1에 가까워지는 값으로, 이 경우에는 0.85로 주어졌습니다.
소성단면계수(Zx)는 단면이 얼마나 강하게 파괴에 저항하는지를 나타내는 값으로, 단면의 넓이와 회전반경의 제곱을 나눈 값에 형상계수를 곱한 값입니다. 이 경우, 단면의 넓이는 1000mm × 500mm = 500000mm2이고, 회전반경(rx)=500√3 mm, 형상계수(f)=0.85이므로, 소성단면계수(Zx)=(500000mm2 / (500√3 mm)2) × 0.85 = 1.5×108mm3입니다.



